 | Повседневная работа современного программиста редко открывает простор для развития творческого мышления. Чаще всего, для решения задач нам достаточно применить проверенное временем решение: паттерн или библиотеку. Знание общепризнанных подходов и практик, библиотек и фреймворков, вот что сегодня является признаком квалификации программиста. Между тем, красота и волшебство программирования для многих (я уверен, что не одинок в этом) в полной мере раскрывается в решении сложных алгоритмических задач, так редко встречающихся в повседневной практике. И раз уж "гора не идет к Магомету", то Магомет придумает себе задачку самостоятельно! UPD: проект переехал в новый репозиторий: https://github.com/programming086/fifteenpuzzle |
В качестве задачки для разминки мозгов, я предлагаю попытаться научить компьютер собирать известную головоломку "Пятнашки".
Пятна́шки — популярная головоломка, придуманная в 1878 году Ноем Чепмэном. Представляет собой набор одинаковых квадратных костяшек с нанесёнными числами, заключённых в квадратную коробку. Длина стороны коробки в четыре раза больше длины стороны костяшек для набора из 15 элементов (и в три раза больше для набора в 8 элементов), соответственно в коробке остаётся незаполненным одно квадратное поле. Цель игры — перемещая костяшки по коробке добиться упорядочивания их по номерам, желательно сделав как можно меньше перемещений.
Ключом, к решению поставленной задачи, станет известный алгоритм поиска по первому наилучшему совпадению на графе А*. Чтобы несколько упростить изложение задачи, я буду рассматривать головоломку с полем размером 3х3.
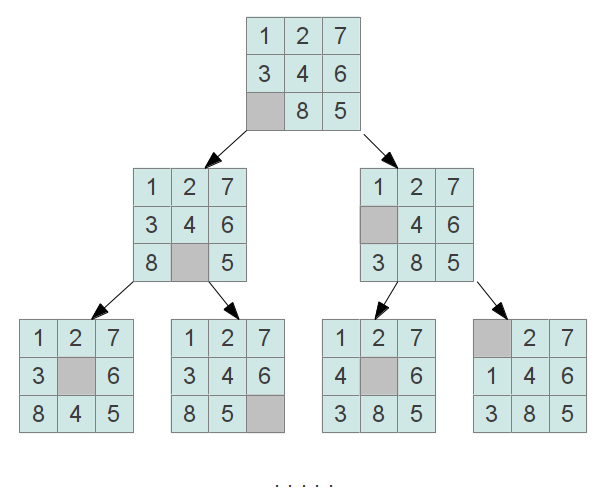
Весь процесс поиска решения в "Пятнашках" можно представить как задачу поиска на графе. Вершинами такого графа будут состояния поля головоломки, полученные в результате перемещения костяшек:
Для решения задачи поиска терминальной вершины на графе можно использовать алгоритмы полного перебора (поиск в глубину или ширину), но количество возможных решений (возможных перестановок) скорее всего окажется на столько велико, что результат полного перебора не удастся увидеть до пенсии.
Алгоритм A* позволяет существенно сократить количество состояний для перебора, путем применения некоторой дополнительной информации, эвристики. В качестве такой информации предлагается брать предполагаемое количество перестановок, необходимых для получения терминального состояния.
Чтобы разобраться, как именно A* позволяет выполнять поиск на графе, рекомендую прочитать статью Алгоритм A* для новичков. Материала на тему этого алгоритма написано так много, что у меня нет желания останавливаться на изложении деталей его реализации, но тем не менее, для дальнейшего понимания происходящего понимание алгоритма A* необходимо. Поэтому, вкратце, я все таки изложу последовательность действий, предпринимаемых алгоритмом, для поиска терминального состояния на примере решения выбранной головоломки.
Алгоритм A* предполагает наличие двух списков вершин графа: открытого и закрытого. В первом находятся вершины, еще не проверенные алгоритмом, а во втором те вершины, которые уже встречались в ходе поиска решения.
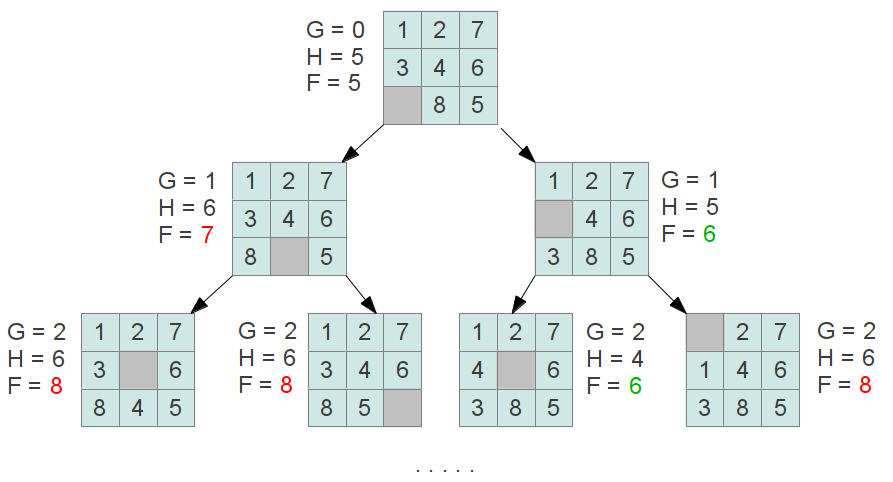
На каждом новом шаге, из списка открытых вершин выбирается вершина с наименьшим весом. Вес (F) каждой вершины вычисляется как сумма расстояния от начальной вершины до текущей (G) и эвристическое предположение о расстоянии от текущей вершины, до терминальной (H). Fi = Gi + Hi, где i - текущая вершина (состояние игрового поля).
Для "Пятнашек" можно сделать предположение, что для достижения терминальной вершины, необходимо выполнить перемещений не меньше, чем количество костяшек, находящихся не на своих местах, а расстояние от начальной вершины до текущей рассчитывать как количество сделанных перестановок:
Выполняется перебор дочерних вершин. Каждая дочерняя вершина проверяется на предмет наличия в списке закрытых. Если вершина не встречалась ранее, она перемещается в список открытых вершин. Для нее рассчитывается эвристическое расстояние до терминальной вершины и пересчитывается расстояние от начальной вершины, ведь есть вероятность, что текущий путь к этой вершине окажется короче, чем найденный ранее (текущая вершина могла уже находится в списке открытых). Если путь оказался короче, ссылка на родительскую вершину изменяется.
Последовательность действий повторяется, пока в списке открытых вершин есть хотя бы одна вершина или пока в ходе выполнения алгоритма не встретится терминальная вершина.
Решение на Java.
Алгоритм А* применим для решения большого числа задач. Мне бы не хотелось ограничивать его реализацию решением только "Пятнашек". Поэтому я предлагаю абстрагироваться от решаемой задачи с помощью интерфейсов, абстрактных классов и наследования.В первую очередь, задачи, решаемые алгоритмом А*, отличаются определением вершин графа (или состояниями). Введем абстрактный класс, инкапсулирующий общее, для любых вершин, поведение:
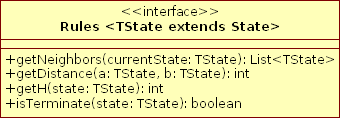
Так же, задачи различаются правилами порождения дочерних вершин, алгоритмом расчета расстояния от начальной вершины и эвристической оценкой расстояния до терминальной вершины. Выделим эти особенности в интерфейс:
import java.util.*;
/**
* Реализует алгоритм поиска решения А*.
*
* @author brovko_rs
*/
public class Astar<TState extends State, TRules extends Rules<TState>> {
/**
* Применяет алгоритм А* для поиска кратчайшего пути до терминального
* состоянияот указанного.
*
* @param startState - начальное состояние.
* @return последовательность состояний от заданного до терминального.
*/
public Collection<State> search(TState startState) {
LinkedList<Integer> close = new LinkedList<Integer>();
LinkedList<TState> open = new LinkedList<TState>();
open.add(startState);
startState.setG(0);
startState.setH(rules.getH(startState));
while (!open.isEmpty()) {
TState x = getStateWithMinF(open);
if (rules.isTerminate(x)) {
closedStates = close.size();
return completeSolution(x);
}
open.remove(x);
close.add(x.hashCode());
List<TState> neighbors = rules.getNeighbors(x);
for (TState neighbor : neighbors) {
if (close.contains(neighbor.hashCode())) {
continue;
}
int g = x.getG() + rules.getDistance(x, neighbor);
boolean isGBetter;
if (!open.contains(neighbor)) {
neighbor.setH(rules.getH(neighbor));
open.add(neighbor);
isGBetter = true;
} else {
isGBetter = g < neighbor.getG();
}
if (isGBetter) {
neighbor.setParent(x);
neighbor.setG(g);
}
}
}
return null;
}
public int getClosedStatesCount() {
return closedStates;
}
/**
* Создает объект для поиска терминального состояния по указанным правилам.
*
* @param rules правила, в соответствии с которыми будет производиться поиск
* терминального состояния.
*/
public Astar(TRules rules) {
if (rules == null) {
throw new IllegalArgumentException("Rules can`t be null.");
}
this.rules = rules;
}
/**
* Находит вершину в списке open с наименьшим значением веса.
*
* @param open список открытых вершин.
* @return вершину с наименьшим весом.
*/
private TState getStateWithMinF(Collection<TState> open) {
TState res = null;
int min = Integer.MAX_VALUE;
for (TState state : open) {
if (state.getF() < min) {
min = state.getF();
res = state;
}
}
return res;
}
/**
* Составляет последовательность состояний пройденных от начального
* состояния до конечного.
*
* @param terminate найденное конечное состояние.
* @return последовательность состояний пройденных от начального состояния
* до конечного.
*/
private Collection<State> completeSolution(TState terminate) {
LinkedList<State> path = new LinkedList<State>();
State c = terminate;
while (c != null) {
path.addFirst(c);
c = c.getParent();
}
return path;
}
private TRules rules;
private int closedStates = 0;
}
Данное решение несколько не оптимально. Наверняка вы заметили, что информация в списке закрытых вершин избыточна: нас никогда не интересуют детали вершин из этого списка, а только факт принадлежности некоторой вершины к нему. Для этого достаточно хранить не сами вершины, а значения их хеш функций. Теперь, что касается реализации непосредственно пятнашек. Я не стану приводить здесь весь исходный код, его вы можете посмотреть в репозитории на github.com. Остановлюсь только на интересных, на мой взгляд, вещах.
Во первых, само игровое поле удобно представить одномерным массивом, это позволит избежать лишних вложенных циклов и в целом упростит решение. Алгоритм раскрытия вершины (получение ее потомков), в таком случае, получается достаточно прост. Вначале находится индекс пустой клетки, затем вычисляется индекс кости, которая будет перемещена на пустую клетку. Ее индекс вычисляется как сумма индекса пустой клетки и индекса одного из ее соседей. Индексы соседних клеток элементарны: для соседа слева это -1, для соседа справа +1, для соседа сверху -(размер поля), для соседа снизу +(размер поля):
private int left = -1;
private int top;
private int right = 1;
private int bottom;
protected int[] actions;
...
top = -sideSize;
bottom = sideSize;
actions = new int[]{top, bottom, left, right};
...
public byte[] doAction(byte[] field, int action) {
/* Выполняется поиск пустой клетки */
int zero = 0;
for (; zero < field.length; zero++) {
if (field[zero] == 0) {
break;
}
if (zero >= field.length) {
return null;
}
}
/* Вычисляется индекс перемещаемой клетки */
int number = zero + action;
/* Проверяется допустимость хода */
if (number < 0 || number >= field.length) {
return null;
}
if ((action == 1) && ((zero + 1) % sideSize == 0)) {
return null;
}
if ((action == -1) && ((zero + 1) % sideSize == 1)) {
return null;
}
/*
* Создается новый экземпляр поля, на котором меняются местами пустая и
* перемещаемая клетки
*/
byte[] newField = Arrays.copyOf(field, field.length);
byte temp = newField[zero];
newField[zero] = newField[number];
newField[number] = temp;
return newField;
}
Во вторых, для генерирования начального состояния, первое, что обычно приходит на ум - это случайное расположение клеток на игровом поле. Но у этого подхода есть существенный недостаток. Если вы уже заглядывали на вики, то знаете, что ровно половину из всех возможных начальных положений пятнашек невозможно привести к собранному виду. То есть, при таком подходе, вы рискуете сгенерировать такое начальное состояние, решение для которого не существует вообще, или поиск решения затянется на неприлично длительное время. Чтобы не портить себе впечатление от проделанной работы, можно пойти другим путем: можно выполнять N случайных, корректных перестановок костяшек, начиная с терминального состояния. Такой подход гарантировано предоставит начальное состояние, обладающее решением и позволит регулировать сложность его поиска:
private static byte[] generateStartState(FifteenRules rules, int swapCount) {
int stepCount = swapCount;
byte[] startState = rules.getTerminateState();
int[] actions = rules.getActions();
Random r = new Random();
while (stepCount > 0) {
int j = r.nextInt(actions.length);
byte[] state = rules.doAction(startState, actions[j]);
if (state != null) {
startState = state;
stepCount--;
}
}
return startState;
}
UPD: По настоятельной просьбе анонимного читателя, я опишу второй, казалось бы очевидный, способ генерирования начального состояния.
Согласно формуле, приведенной на википедии, можно заранее проверить начальное состояние на возможность приведения его к терминальному виду:
Можно показать, что ровно половину из всех возможных 1 307 674 368 000 (=15!) начальных положений пятнашек невозможно привести к собранному виду: пусть квадратик с числомрасположен до (если считать слева направо и сверху вниз)
квадратиков с числами меньшими
, то есть если после костяшки с
. Также введем число
— номер ряда пустой клетки (считая с 1). Если сумма
является нечётной, то решения головоломки не существует.
И в случае, если решения не существует, повторно сгенерировать начальное состояние. Полагаться на волю случая мне не по душе, но выбирать тот или иной подход вам. В любом случае главное решение, а не начальное состояние :)
Процедура проверки начального состояния:
/**
* Проверяет, возможно ли привести состояние к терминальному.
*
* @param field состояние игрового поля.
* @param sideSize размер стороны игрового поля.
* @return true - если можно привести к терминальному.
*
* @see http://ru.wikipedia.org/wiki/Пятнашки
*/
public static boolean checkState(byte[] field, int sideSize) {
int N = 0;
int e = 0;
for (int i = 0; i < field.length; i++) {
/* Определяется номер ряда пустой клетки (считая с 1). */
if (field[i] == 0) {
e = i / sideSize + 1;
}
if (i == 0) {
continue;
}
/* Производится подсчет количества клеток меньших текущей */
for (int j = i + 1; j < field.length; j++) {
if (field[j] < field[i]) {
N++;
}
}
}
N = N + e;
/* Если N является нечётной, то решения головоломки не существует. */
return (N & 1) == 0; // Первый бит четного числа равен 0
}
Чтож, остальные детали реализации не должны вызывать трудностей. Однако, хочу заметить, что предложенная эвристика далека от совершенства. Ее можно усовершенствовать, что позволит сократить количество раскрываемых алгоритмом вершин и, соответственно, ускорить его работу. Буду рад увидеть ваши предложения по развитию эвристической оценки в комментариях.Напоминаю, что целиком мое решение вы можете взять с репозитория:
git clone https://github.com/programming086/fifteenpuzzle.git
или опробовать его в действии: FifteenPuzzle-0.0.1-SNAPSHOT.jar.
Для Unix
java -DconsoleEncoding=UTF-8 -jar FifteenPuzzle-0.0.1-SNAPSHOT.jar -hДля Windows
java -DconsoleEncoding=Cp866 -jar FifteenPuzzle-0.0.1-SNAPSHOT.jar -h
Немає коментарів:
Дописати коментар